Contributed by David Marlowe, Owner/CEO, DMAR Technical Training and DMAR Business Centers USA
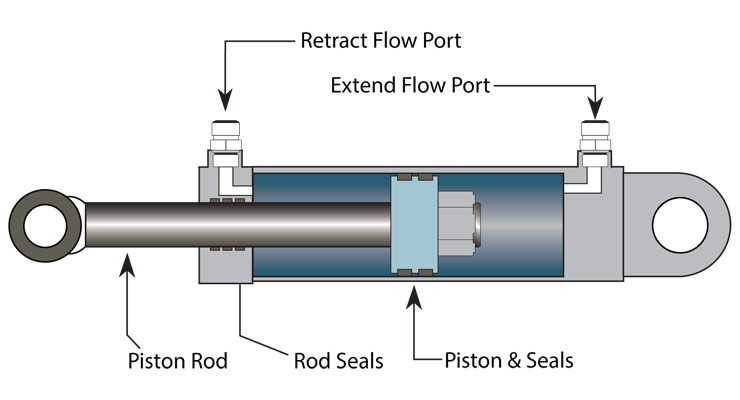 This article will talk about the business end of the hydraulic system: The force produced by the cylinder. When using a standard double-acting cylinder, there are three internal areas of concern:
This article will talk about the business end of the hydraulic system: The force produced by the cylinder. When using a standard double-acting cylinder, there are three internal areas of concern:
- Piston area = transfer fluid pressure to force to extend piston rod
- Net piston area minus piston rod area
- Rod area = significant when cylinder is used in regenerative action
To calculate cylinder force against a load, two calculations are required:
- Force over piston area
- Opposing force over opposing piston area
For example:
- Extension force is 50 psi x 20 in.2 = 1,000 lb.
- Opposing force on rod side is 30 psi x 18 in.2 = 540 lb.
The net force the cylinder can exert against a load in the extension direction is:
1000 lb – 540 lb = 460 lb
It is important to remember and calculate in the added pressure required due to packing friction, which in standard cylinders can amount to 5% (let’s say 10%, to be safe) of the maximum force for which the cylinder is rated. This extra power is consumed when the cylinder is in motion.
Cylinders are designed to move various types of loads:
Vertical gravity load—a non-friction load that requires full cylinder force to be produced throughout the stroke. Additional force will be required and calculated in to accelerate the load and to overcome loss due to supply flow and friction losses.
 Stall-out load—in cylinders that are used on either vertical or horizontal presses, when the press contacts the work piece the cylinder stalls. During cylinder piston movement, they usually run in “free traverse” for most of the stoke. During free traverse, very little pressure is required on the cylinder piston and the pump supplies only the hydraulic circuit losses due to fluid flow friction. At stall, all fluid flow friction disappears. When calculating pressures required at the cylinder port, allow 5% for packing friction losses even with no movement through the packing.
Stall-out load—in cylinders that are used on either vertical or horizontal presses, when the press contacts the work piece the cylinder stalls. During cylinder piston movement, they usually run in “free traverse” for most of the stoke. During free traverse, very little pressure is required on the cylinder piston and the pump supplies only the hydraulic circuit losses due to fluid flow friction. At stall, all fluid flow friction disappears. When calculating pressures required at the cylinder port, allow 5% for packing friction losses even with no movement through the packing.
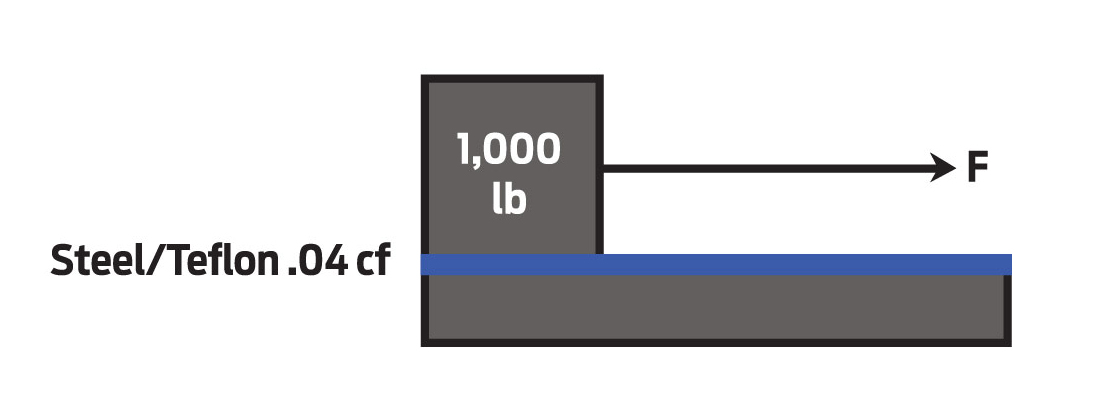
Horizontal friction loads—horizontal cylinders can be used for either push or pull applications.
- Push application is acceleration away from source.
- Pull application is acceleration towards source.
The force required for moving a load horizontal is less than the force required to lift it. To calculate for a horizontal load, you have to calculate the load times the static coefficient of static friction (resistance to movement created by molecular attraction between load and surface materials)
 Static coefficient of materials can be obtained from a machinery handbook.
Static coefficient of materials can be obtained from a machinery handbook.
Rolling loads—we all know how much a wheel makes it easier to move an object across a surface. By replacing sliding resistance with rolling resistance, you require a significant amount less force. With rolling load, there will be a breakaway force required to set the load in motion; a force as little of 1⁄10 the load will break away the load and then even less force is required to keep the load in motion. The breakaway load is caused by the wheel as it applies a force on the surface material. The displaced material from under the wheel is pushed out in front of the wheel. As the wheel moves across the surface, it continually displaces the surface material to the front of the wheel creating the rolling resistance. If you roll a wheeled chair across the carpet, you can see the carpet bulge up in front of the wheel. Even though we are rolling hardened steel across a steel surface, the steel will act just like the carpet.
Punching loads—the cylinder application is used to punch, shear or notch a work piece.
Use the following calculation:
A (area to be sheared) = (L + W + L + W) x T
All dimensions must be in inches
 After calculating the number of square inches of metal to be sheared, multiply that number times the shear strength of the material. This gives the cylinder force needed to make the cut.
After calculating the number of square inches of metal to be sheared, multiply that number times the shear strength of the material. This gives the cylinder force needed to make the cut.
Shear strength for metal can be assumed to be about 75% of the metals rated tensile strength and is expressed in psi. For accurate shear values, consult the supplier of the material.
DMAR Technical Training
dmartechtraining.biz
Filed Under: Cylinders & Actuators, Mobile Hydraulic Tips
